Cracker algorithm for mining connected components in large graphs accepted at ISCC 2015!
Accepted at the 20th IEEE Symposium on Computers and Communications, Larnaca, Cyprus, 6–9 July 2015 [1].
Abstract. The problem of finding connected components in a graph is common to several applications dealing with graph analytics, such as social network analysis, web graph mining and image processing. The exponentially growing size of graphs requires the definition of appropriated computational models and algorithms for their processing on high throughput distributed architectures. In this paper we present cracker, an efficient iterative algorithm to detect connected components in large graphs. The strategy of cracker is to iteratively grow a spanning tree for each connected component of the graph. Nodes added to such trees are discarded from the computation in the subsequent iterations. We provide an extensive experimental evaluation considering a wide variety of synthetic and real-world graphs. The experimental results show that cracker consistently outperforms state-of-the-art approaches both in terms of total computation time and volume of messages exchanged.
1 The cracker Algorithm
The basic idea of cracker is to iteratively reduce the graph size by progressively pruning vertices until only one vertex for each connected components (CC) is left, i.e., its seed. For instance, an isolated vertex can be immediately excluded from further processing, since it does not provide useful information for the discovery of the other ccs. Similarly, as soon as a cc is identified, it can be excluded from computation since it does not impact on the other ccs in the graph. When a vertex is removed, it contributes to iteratively build a spanning tree that, at the end of the algorithm, will exist a spanning tree for each connected component.
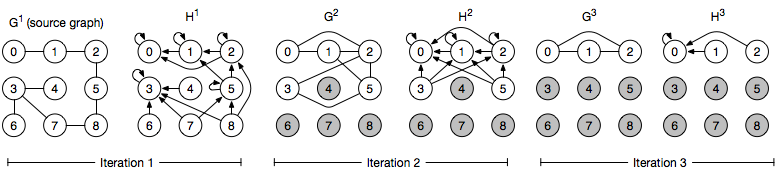
The seed identification is an iterative algorithm made of two steps. The first step, named Min Selection Step, aims at understanding, for each node, if it is a potential seed by at least one of its neighbours. This decision is taken locally at each node, given that the only knowledge available locally to each node is its neighbourhood. A node can be considered as a potential seed if it is a local minimum in the neighbourhood of some node. If a node is not a local minimum in any neighbourhood then it cannot be a seed. To identify such nodes, the information about the local minimum in its neighbourhood is spread by each node to its neighbourhood.
Given the undirected input graph Gt, an intermediate directed graph Ht is generated linking nodes to potential seeds. Subsequently, the goal of the Pruning Step is to remove from Ht, and thereby deactivate, all the nodes that cannot be considered as seeds. A new undirected graph Gt+1, smaller that Gt, is generated and used to feed the next iteration (see Figure 1). The nodes that are moved during the Pruning Step grow a forest of covering trees T of the cc in the graph. Eventually, the seeds remain the only active nodes in the computation. Upon their deactivation, the Seed Identification terminates and the Seed Propagation is triggered.
2 Experiments
| Italy | California | PPI-All
| ||||||||||
| Algorithm | Time | Steps | Msg.s | Vol. | Time | Steps | Msg.s | Vol. | Time | Steps | Msg.s | Vol. |
| cracker | 461 | 33 | 726 | 1724 | 37 | 24 | 54 | 132 | 1389 | 12 | 885 | 2134 |
| ccf | 807 | 18 | 1214 | 4744 | 60 | 14 | 100 | 408 | 2182 | 6 | 239 | 3733 |
| hash-to-min | 1681 | 18 | 1774 | 6456 | 87 | 14 | 147 | 539 | 1777 | 6 | 1103 | 4360 |
| ccmr | >3957∗ | >15∗ | – | – | 88 | 14 | 197 | 333 | 2235 | 6 | 3099 | 5174 |
| | ||||||||||||
| Flickr | YouTube | Skitter
| ||||||||||
| Algorithm | Time | Steps | Msg.s | Vol. | Time | Steps | Msg.s | Vol. | Time | Steps | Msg.s | Vol. |
| cracker | 45 | 12 | 60 | 147 | 43 | 15 | 68 | 164 | 35 | 14 | 50 | 126 |
| ccf | 54 | 7 | 40 | 239 | 49 | 7 | 65 | 267 | 38 | 7 | 39 | 193 |
| hash-to-min | 82 | 7 | 90 | 338 | 113 | 7 | 109 | 394 | 77 | 7 | 82 | 305 |
| ccmr | 107 | 6 | 170 | 287 | 211 | 7 | 140 | 239 | 127 | 7 | 151 | 255 |
| pegasus | 121 | 14 | 459 | 1354 | 140 | 19 | 417 | 1191 | 136 | 21 | 501 | 1469 |
Experimental results on real-word data are shown in Table 1. cracker resulted to be the most efficient algorithm. The wide spectrum of datasets analysed reveals that the pruning mechanism is effective and lets cracker to outperform the existing state-of-the-art solutions. cracker revealed to be a very flexible solution, resulting the most efficient solution both when the largest cc is near the dimension of the entire graph and when it is of smaller size. In terms of time, cracker outperforms its competitors in every dataset used, with the best competitor being from 9% to 75% slower. Finally, cracker obtained the least message volume among all the competitors.
