Speeding up Document Ranking with Rank-based Features
Accepted as short paper at the 38th International ACM SIGIR Conference on Research and Development in Information Retrieval, Santiago de Chile, 9–13 August 2015 [1].
Abstract. Learning to Rank (LtR) is an effective machine learning methodology for inducing high-quality document ranking functions. Given a query and a candidate set of documents, where query-document pairs are represented by feature vectors, a machine-learned function is used to reorder this set. In this paper we propose a new family of rank-based features, which extend the original feature vector associated with each query- document pair. Indeed, since they are derived as a function of the query- document pair and the full set of candidate documents to score, rank-based features provide additional information to better rank documents and return the most relevant ones. We report a comprehensive evaluation showing that rank-based features allow us to achieve the desired effectiveness with ranking models being up to 3.5 times smaller than models not using them, with a scoring time reduction up to 70%.
Rank-based Features
| q1 | q2 | q3
| ||||||
| rel | BM25 | PR | rel | BM25 | PR | rel | BM25 | PR |
| 1 | .80 | .20 | 1 | .60 | .50 | 1 | .65 | .45 |
| 1 | .75 | .15 | 1 | .60 | .47 | 1 | .67 | .40 |
| 0 | .65 | .05 | 1 | .50 | .45 | 0 | .60 | .35 |
| 0 | .65 | .05 | 0 | .45 | .40 | 0 | .40 | .15 |
To introduce the new set of rank-based features, let us consider the example in Table 1. The table illustrates a small training set of query-document feature vectors. It is made up of three queries with four candidate results each. For each document associated with a query, a binary relevance label rel and two well-known features – BM25 and PageRank (PR) – are listed. During learning, a tree-based algorithm should find the rules that best separate relevant from irrelevant results. A simple decision stump – i.e., a tree with one node and two leaves – is not sufficient in this case, since a “minimal” classification tree with perfect accuracy is the following:
if BM25 ≥ .75 then 1 else
if PR ≥ .45 then 1 else
if BM25 ≥ .67 then 1 else 0
Simpler but still effective trees can be obtained if we enrich the feature set associated with each pair (q,c), c ∈𝒞q, with new rank-based features. In our toy example, an optimal decision tree that achieves perfect accuracy is the one that classifies as relevant the documents with a PR score being at most 0.05 less than the best PR score in the same candidate set, that is:
if Dist-Max PR ≤ 0.05 then 1 else 0
where Dist-Max PR measures the difference between each value of PR and the largest value assumed by PR in 𝒞q. This last classifier does not improve the quality of the first one. On the other hand, it is much simpler and its evaluation requires much less time if rank-based features are available.
We propose four construction strategies to build new rank-based features for a given feature f ∈ℱ, occurring in the feature vector representing each pair (q,c), where c ∈𝒞q:
- Rank f. Feature Rank f ∈ {1,2,…,|𝒞q|} corresponds to the rank of c after sorting 𝒞q in descending order of f.
- Rev-Rank f. The same as Rank f, but 𝒞q is ordered in ascending order of f.
- Dist-Min f. Feature Dist-Min f ∈ ℝ is given by the absolute value of the difference between the value of f and the smallest value of f in 𝒞q.
- Dist-Max f. The same as Dist-Min f, but we consider the difference with the largest value of f in 𝒞q.
We expect that these new features can improve the scoring ability of the learned models since they contribute to give information about the whole set of candidates Cq, while other features give information limited to the single pairs (q,c) with respect to the entire collection of indexed documents. We claim that they can capture relatively better or relatively worse concepts over the current candidate set. It is worth noting that Rank f and Rev-Rank f are not mutually exclusive. If higher values of f are better, the former could promote good documents, while the latter should demote bad documents.
Efficiency of learned models
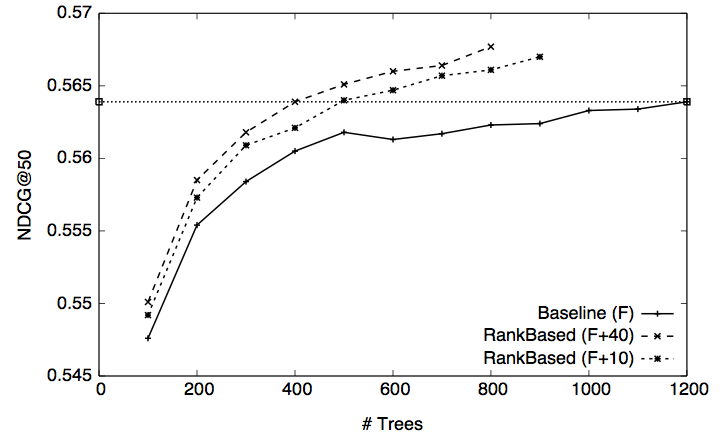
Figure 1 illustrates the quality in terms of NDCG of the λ-MART models trained on MSN/Fold 1 by using ℱ, ℱ+40, and ℱ+10 (respectively the original feature set, and extended feature sets adding 40 or 10 rank-based features). We report the values of NDCG@50 obtained on the test set of MSN/Fold 1 as a function of the number of trees of the generated model. Note that the three curves stops in correspondence of a different number of trees: this is because the validation set is used to choose the number of trees in the final model.
The benefit of our rank-based features shows up very early in the learning process. First, we note that the new feature sets ℱ+40 and ℱ+10 always produce models that are more effective than the one obtained by using the original feature set ℱ at smaller ensemble sizes. More importantly, the maximum quality of the model trained on ℱ requires a number of trees that is about three times larger than the number of trees of the models trained on either ℱ+40 or ℱ+10 to obtain the same NDCG@50. This behaviour is very significant, since the number of trees directly impacts ranking efficiency. Document scoring requires in fact the traversal of all the trees of the model, and its cost is thus linearly proportional to their number.